A neural network learns relationships between inputs and the corresponding outputs from sample data, it then applies the learnings to new inputs to predict the best possible outputs.
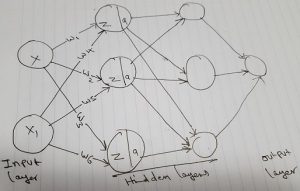
Neural Network
Weights and bias
A Neural network consists of neurons and one or more layers. As in the pic above, weights (w) connect neurons from one layer to the next and represent the importance of a given input to its respective output.
For example, how important are the following inputs to decide where to go for a vacation?
1.Price of tickets (w=1)
2. Price of hotels (w=1)
3. Weather (w=0)
Higher weight means more importance.
While weights represent the importance, bias is used to fine-tune the relationship between inputs and outputs.
A neuron computes the weighted sum of its inputs, adds bias to compute (z) and passes the z to the activation function (a) to get a single output. A neural network learns by collecting these outputs from each neuron; this is done by doing forward propagation, getting the loss, and updating w and b to decrease the loss (backward propagation).
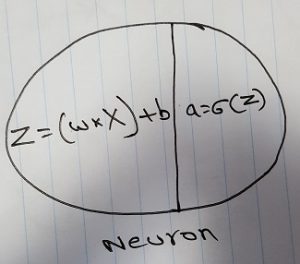
Neuron
Forward Propagation
Neural Network (NN) takes an input x from the input layer, it multiplies it with its respective weight, adds bias to it and passes the resulting value to an activation function. The resulting value is then passed to the next layer as an input.
z = w * x + b and z passed to, a = sigmoid(z)
At the end of the forward propagation, the output layer results in a predicted value, then we compare the predicted value with the actual value to figure out the difference, and update w and b to decrease the difference. This process is repeated multiple times to get to the prediction we like.
In the next posts, we will discuss activation functions, cost functions, and backward propagation.

